Winding numbers using a Cauchy integral, with WebGL
This is what the winding number
$$ n(\gamma ,a) = \frac{1}{2 \pi i}\int_{\gamma}^{}\frac{1}{z-a}dz $$
Demo
(drag your mouse/thumb across the red canvas)
Each pixel displays its complex winding number: Real part as Hue, Imaginary part as Luminance. Curves can be drawn with mouse dragging, some predefined shapes are available.
The formula
Along the way to proving Cauchy’s Integral Formula, there’s this winding number which I find remarkable. Out of seemingly innocuous operations on complex numbers it always outputs a real integer number; And it mysteriously is the number of turns a curve takes around a point! But the curve has to be closed.
Do not ask me to intuitively explain why it does that. In fact, I built this visualization to tinker with this formula and investigate. You can go over there to try to make sense of it.
But what if you don’t close the loop? Turns out the formula outputs ‘undefined’, in the form of a complex part to the winding number. One area is positive (high luminance) if it had too much ‘going to’ and negative (low luminance) if too little. To make the canvas mostly Real, you want to go from areas in need of ‘going to’ to areas that have too much of it, closing the loops! So the formula even comes with a debug function.
Of note is that the inverse of a curve is the same curve going backwards: same integral, replace
This means you can split a bigger curve in two by adding a back and forth between two points on it, re-arranging the integrals. It is equivalent to identity, as you just added a curve and its inverse. And vice versa: merge two compatible smaller curves into a bigger one.
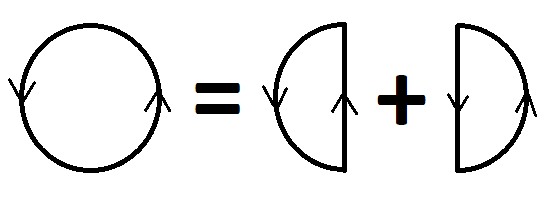
Sort of, minus the visual glitches
Visual glitches
Precision can be tuned so that smaller or bigger
On mobile you may experience inaccurate winding numbers: non-smooth colors inside closed loops. This is due to intermediate results being written to float textures, and WebGL on mobile often only has 4 bits per channel when desktop offers 16 bits.
Code
Building it
Well, if you want a ~500x500 pixel canvas for a curve of about 1000 elements that’s already 250 million operations; this gives a great opportunity to use the GPU.
I use two fragment shaders. One for projecting the real and imaginary parts -which I store as the red and green channels in a texture- onto a hue-saturation-luminance space. I chose hue for the real part as it illustrates about the ’nature’ of the output; while we want some kind of fading out of this clear result when we get too imaginary. So luminance seemed like a better fit for the imaginary part, and saturation is constant. Hue is scaled in order that a round number of windings (12) gets you back to red.
The other fragment shader contains the formula, and I switch back and forth between reading and writing to two textures to accumulate the sum. Programming in glsl/WebGL feels refreshingly simple with its SIMD nature. In goes a single (x,y) pixel coordinate, and the programmer is tasked with defining what the outgoing color for this single pixel is:
void main(void) {
vec2 a = gl_FragCoord.xy / 512.0; # scale xy
vec2 prev = texture2D(u_calcSamp, a).xy; # fetch previous value
# compute Cauchy formula
vec2 delta = a - u_z;
float denom = dot(delta, delta);
gl_FragColor = vec4( # output is rgba
prev.x + (delta.x * u_dz.y - delta.y * u_dz.x) / denom, # real in red
prev.y + dot(delta, u_dz) / denom, # imaginary in green
1.0,
1.0
);
}If you want to start tinkering with glsl/WebGL, I highly recommend you checkout Shadertoy.
I also monitor time between animation frames, and cram in as many calculation cycles as possible while trying to maintain at most 40 ms between frames.
And that’s about all there is to it; the rest is glue code, UI, and basic features.