Indice d’une courbe autour d’un point avec une Intégrale de Cauchy, en WebGL
Voici une visualisation de l’indice -le nombre de tours-
$$ n(\gamma ,a) = \frac{1}{2 \pi i}\int_{\gamma}^{}\frac{1}{z-a}dz $$
Demo
(faites glisser la souris/le pouce sur la surface rouge)
Chaque pixel affiche par sa couleur son indice: la partie réelle donne la teinte, la partie imaginaire la luminance. Des formes prédéfinies sont mises à disposition.
La formule
Pendant la démonstration de la Formule intégrale de Cauchy, on tombe sur une formule remarquable. Formée à partir de composantes innocentes complexes, elle donne toujours un nombre entier et réel. De plus, assez mystérieusement, elle indique le nombre de tour que la courbe fait autour du point! Mais on exige que la courbe soit fermée sur elle-même.
Ne me demandez pas une explication intuitive du phénomène: À vrai dire j’ai construit cette visualisation pour essayer de m’en faire une idée. Vous pouvez tenter de construire la votre à partir de ces réponses.
Du coup, que se passe-t-il si on ne referme pas la boucle? Eh bien la formule nous renvoie une ’erreur’, sous la forme d’un nombre qui comporte désormais une partie imaginaire. Une zone devient positive et demande qu’on parte de ce point (luminance élevée), ou bien négative (faible luminance) si il faut qu’on y aille. On peut alors ‘rendre le plan réel’ en allant des parties lumineuses vers les sombres et effectivement clore les courbes sur elle-mêmes. La formule est fournie avec sa propre fonction de debogage!
On notera que l’inverse d’une courbe est la même courbe mais parcourue en sens inverse: on remplace
Ceci signifie qu’on peut diviser une plus grande courbe en deux par un aller-retour entre deux de ses points, en réarrangeant les intégrales. Cette opération est l’identité, puisqu’on vient seulement de rajouter une courbe et son inverse. Et vice versa, on peut fusionner deux courbes ayant un bord commun en une plus grande.
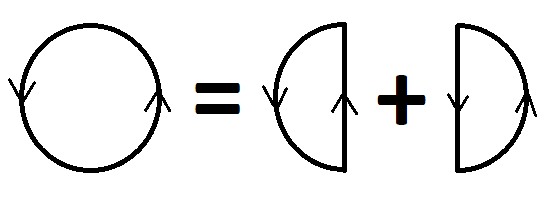
Diviser une courbe, si on regarde pas les artéfacts
Artéfacts
On peut configurer des niveaux de précision pour utiliser des
Sur mobile il se peut que vous ne voyiez pas de surface unie sur des courbes fermées. C’est dû au fait que les résultats intermédiaires sont stockés dans des textures en nombres flottants, et que WebGL ne donne que 4 bits sur mobile, alors qu’il en fournit 16 sur Desktop.
Code
Construction
Bon, si vous voulez un calcul sur une zone de ~500x500 pixel pour une courbe de 1000 éléments, on est déjà à 250 million d’opérations; l’utilisation d’un GPU est donc pluc adaptée.
J’utilise deux fragment shaders. Un pour projeter les parties réeles et imaginaires, que je stocke dans les channels rouge et vert, dans un espace teinte-saturation-luminance. J’ai choisi la teinte pour la partie réelle parce qu’elle illustre un ‘degré de situation’ pour un point. On voudra commenter la cohérence de cette situation dans un sens ou un autre: ce sera donc la luminance pour la partie imaginaire. Et on met une saturation constante. La teinte est coefficientée de telle sorte qu’un nombre entier de tours (12) nous ramène au rouge.
L’autre fragment shader contient la formule, et deux textures sont interverties en lecture-écriture pour accumuler la somme. La programmation en glsl/WebGL est admirablement claire avec sa nature SIMD; On donne les coordonnées (x,y) d’un pixel, et charge au programmeur de déterminer la couleur de ce pixel:
void main(void) {
vec2 a = gl_FragCoord.xy / 512.0; # mise à l'echelle de xy
vec2 prev = texture2D(u_calcSamp, a).xy; # valeur précedente
# formule de Cauchy
vec2 delta = a - u_z;
float denom = dot(delta, delta);
gl_FragColor = vec4( # rgba en sortie
prev.x + (delta.x * u_dz.y - delta.y * u_dz.x) / denom, # réel en rouge
prev.y + dot(delta, u_dz) / denom, # imaginaire en vert
1.0,
1.0
);
}Si programmer en glsl/WebGL vous tente, je recommande vivement le site Shadertoy.
Par ailleurs je mesure le temps entre deux animation frames, et met autant de cycles de calcul que possible en essayant de ne pas dépasser 40ms entre deux frames.
C’est à peu près tout, le reste du code est de la colle, de l’UI, et des fonctionalités classiques.